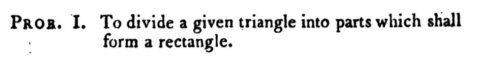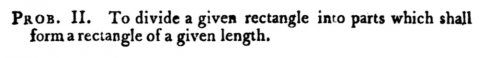Rubrique: Accueil > Vers le supérieur > Les conférences de l’université
Les figures ne manquent pas d’aire
Voici un article conçu et rédigé par Guillaume Moussard, à la suite de la conférence qu’il a donnée ce mercredi 22 novembre à l’ESPE
Partons d’un constat que l’on peut tirer par exemple de la consultation des manuels scolaires : la notion d’aire est enseignée plus souvent comme une notion numérique que comme une notion géométrique. Ainsi de la comparaison des aires en comparant des nombres (en l’occurrence des mesures de leurs aires, étant donnée une unité d’aire), du théorème de Pythagore en calculant des racines carrées à la calculatrice ou encore du théorème de Thalès ramené le plus souvent à des calculs de quatrième proportionnelle de … nombres ! Pourtant, explorer l’aire d’une figure comme une notion géométrique permet d’en construire le sens et donne lieu à de nombreuses activités amusantes et surtout propices au raisonnement.
Le livre I des Eléments d’Euclide (IIIe siècle av. J.C.) présente plusieurs théorèmes sur les aires des figures, démontrés sans jamais recourir aux nombres. En voici deux.
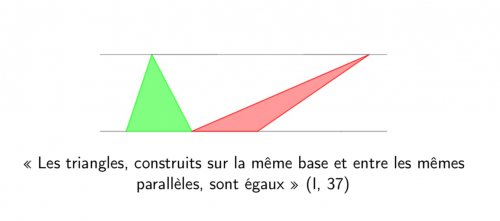
Proposition 37 : les triangles, construits sur la même base et entre les mêmes parallèles sont égaux entre eux.
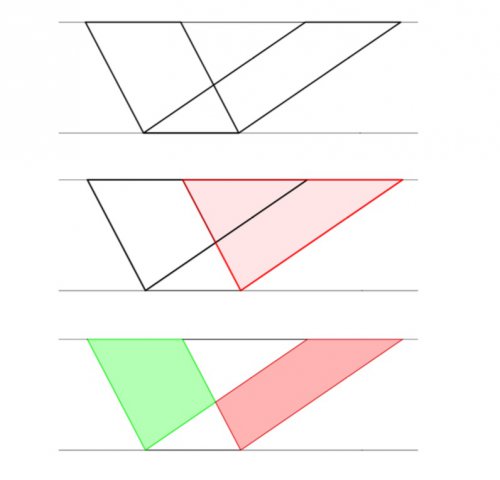
Ce résultat est d’abord démontré pour les parallélogrammes : des parallélogrammes construits sur la même base et entre les mêmes parallèles sont égaux entre eux. L’observation de la succession de figures suivantes permet de s’en convaincre :
La figure des deux parallélogrammes (en haut) peut être regardée comme constituée de deux triangles superposables et donc égaux (au milieu). Si on retire à ces triangles leur partie commune, les quadrilatères restants sont égaux (en bas). Si on ajoute à ces quadrilatères un même triangle, on obtient les deux parallélogrammes de départ, qui sont par conséquent égaux. De ce résultat sur les parallélogrammes, on déduit facilement celui annoncé sur les triangles, qui sont des moitiés de parallélogrammes.
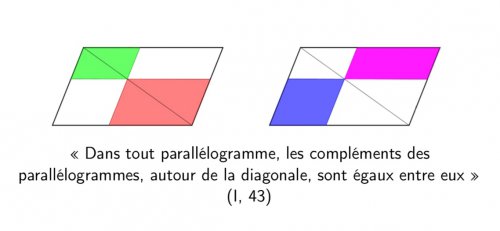
Proposition 43 : Dans tout parallélogramme, les compléments des parallélogrammes, autour de la diagonale, sont égaux entre eux.
Ci-dessus, les parallélogrammes bleu et violet sont égaux. En effet, la diagonale partage en deux parties égales le grand parallélogramme, ainsi que le vert et le saumon. Les parallélogrammes bleu et violet sont donc chacun égaux à la moitié du grand parallélogramme moins la moitié du vert et la moitié du saumon. Ils sont donc égaux. Remarquons que cette figure permet de construire, un parallélogramme étant donné (le bleu), un autre parallélogramme (le violet) de même aire et dont un côté est donné.
Ces deux propositions n’ont rien d’évident à priori. Pourtant chaque pas menant à leur démonstration est parfaitement évident. Ce paradoxe a amené Henri Poincaré à se demander « comment se fait-il qu’il y ait des gens qui ne comprennent pas les mathématiques ? »], autrement dit à quel moment nos affirmations ont-elles perdu leur caractère d’évidence ?
Les propositions du premier livre des Eléments d’Euclide permettent de comparer les aires de deux figures rectilignes (polygones) quelconques, en établissant la construction à la règle et au compas d’un rectangle de largeur donnée et égal à un polygone donné. Dès lors, on compare les aires de deux polygones en comparant les longueurs des rectangles obtenus avec chacun d’eux. Les propositions que nous avons présentées ci-dessus sont au cœur de cette construction.
Au XIXe siècle, William Wallace pose dans le journal de mathématiques anglais New series of the mathematical repository un problème portant sur la notion d’aire :
De deux polygones de même aire, peut-on découper l’un en un jeu de triangles permettant de reconstituer l’autre ?
La réponse, affirmative, est apportée par John Lowry qui ramène la question à la résolution des deux problèmes suivants :
En effet, si l’on sait diviser un triangle quelconque pour recomposer un rectangle, puis diviser un rectangle quelconque pour recomposer un autre rectangle de longueur imposée, alors deux triangles de même aire peuvent être décomposés en deux rectangles superposables et la superposition des deux découpages répond à la question.
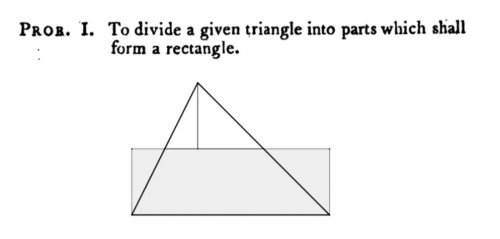
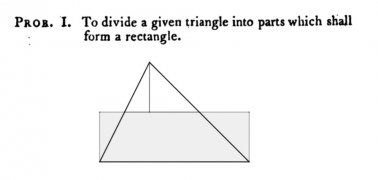
John Lowry répond au premier problème en traçant la hauteur du triangle, puis la parallèle à sa base coupant cette hauteur en son milieu :
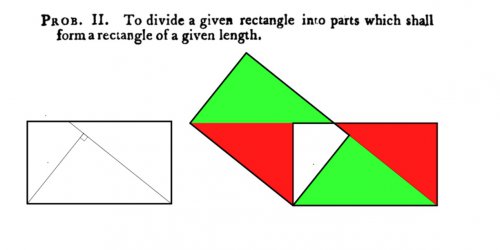
Il répond au second problème en traçant la longueur imposée à partir d’un sommet du rectangle donné, puis la perpendiculaire à cette ligne passant par un autre sommet du rectangle :
Le réarrangement des trois morceaux obtenus aboutit à un rectangle (oblique sur la figure) dont la longueur est bien égale à la longueur donnée. Cette figure peut donner lieu à un pavage du plan constitué de deux familles de rectangles, les uns horizontaux, et les autres obliques.
On trouve parmi les 23 problèmes posés par David Hilbert en 1900 au deuxième congrès international des mathématiques l’équivalent du problème ci-dessus mais posé cette fois-ci dans l’espace. Plus exactement, Hilbert est convaincu qu’il n’est pas possible, étant donnés deux polyèdres de même volume, de découper l’un en un jeu de polyèdres permettant de reconstituer l’autre.
C’est le troisième de ces problèmes censés orienter et stimuler la recherche mathématique du XXe siècle. Il est résolu dès l’année suivante par un assistant de Hilbert, Max Dehn, qui introduit dans sa démonstration un invariant, c’est-à-dire une grandeur algébrique dont la valeur reste inchangée lorsqu’on décompose et recompose un polyèdre. Or cet invariant prend des valeurs distinctes pour un cube et un tétraèdre, il est donc impossible de décomposer l’un pour reconstituer l’autre. Cet invariant prend la forme d’un produit tensoriel de R×R/πZ :
où l1, l2 … ln sont les longueurs des arêtes du polyèdre, et α1, α2 … αn sont les angles dièdres entre les paires de faces correspondantes.
Référence :
Jean-Pierre Friedelmeyer, « Equidécomposabilité des polygones plans », L’ouvert, 117, 2008.
André Pressiat, « Découpages et recomposition pour les aires et les volumes ».
Daniel Perrin, « Aire et volume : découpage et recollement », Images des maths, 2010.
Mise à jour : 15 décembre 2017