 |
solutions des exemples de questions |
05-01-2005 |
l'opération * définie par a*b = 1/ab (1978 : J20, I09 et S06)
(a*b)*c=(1/ab)*c=1/[(1/ab)c]=ab/c alors que a*(b*c)=a*(1/bc)=1/[a(1/bc)]=bc/a
le carré déformé en rectangle (1981 : J16)
Choisissons un carré de côté 10 ; alors l'aire du rectangle vaut 9x11=99, soit 99/100=99% de l'aire du carré.
le décompte des triangles équilatéraux (1984 : J27, I27 et S24)
Classons les triangles selon leur taille : 9 "petits" de côté 1 (par commodité), 3 "moyens" de côté 2, et le "grand" de côté 3.
Ne pas oublier les deux triangles de côté "racine de 3" qui forment une étoile de David ! Réponse : (9+3+1)+2=15
De même pour les carrés : (9+4+1)+(4+2)=20 (4 carrés de côté "racine de 2", et 2 de côté "racine de 5"),
et 9+(4+2+4+2)=21 (4 carrés de côté "racine de 2", 2 de côté "racine de 5", 4 de côté "racine de 8", et 2 de côté "racine de 13").
Remarque : Le triangle équilatéral (ou équiangle, ces deux propriétés sont équivalentes) est le triangle régulier. De même le carré est le quadrilatère régulier, mais le quadrilatère équilatéral est le losange et le quadrilatère équiangle convexe est le rectangle (attention ! il existe des quadrilatères équiangles croisés) ; le carré est donc à la fois un losange et un rectangle.
les mélanges d'eau et de vinaigre (1988 : I12 et J17)
Les proportions d'eau et de vinaigre sont respectivement (2/3 et 1/3) et (3/4 et 1/4). Dans le mélange on aura donc 2/3+3/4=17/12 d'eau et 1/3+1/4=7/12 de vinaigre, soit 17 pour 7.
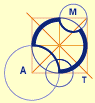
géométrie d'un triangle (1990 : J14, I9 et S4)
PQR est isocèle en P ; ses deux autres angles valent (180°-20°)/2=80°. PQS est isocèle en Q ; son angle au sommet vaut 180°-2x20°=140°. L'angle du secteur (RQS) vaut donc 140°-80°=60°.
la somme du plus grand et du plus petit (1991 : J8 et I4)
0,7+ 0,302=1,002 (question très mal réussie : beaucoup d'élèves pensent que l'ordre dépend du nombre de décimales et trouvent 0,688+0,7=1,388 !)
la boisson à l'orange (1991 : I14 et S11)
Soit v le volume en ml de jus d'orange à ajouter ; on a alors (100+v)/(1000+v)=50%=1/2 soit v=800
le petit rhombicosidodécaèdre (1996 : J29 et I25)
Une arête est formées de deux côtés de deux faces, d'où (12x5+20x3+30x4)/2=120
Le petit rhombicuboctaèdre a 26 faces (8 triangulaires et 18 carrées). Il a donc (8x3+18x4)/2=48 arêtes, et d'après la formule d'Euler s=a-f+2=48-26+2=24 sommets.
Pour le petit rhombicosidodécaèdre on obtient s=120-62+2=60 sommets.
le disque découpé en neuf régions (2000 : I28 et S27)
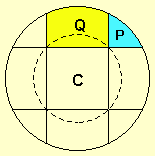
| Une corde partage l'aire A du disque dans le rapport 1/3 (ce que nous avons coutume d'appeler "proportionnellement à 1 et 3"), donc en deux parties d'aires A/4 et 3A/4 (et non "au tiers" ce qui donnerait des parties d'aires A/3 et 2A/3, donc un rapport 1/2).
Il suffit alors d'écrire que l'aire d'une "bande centrale" 2Q+C=A/2 est égale au double de l'aire d'une "bande extrême" 2P+Q=A/4, d'où l'aire du carré central C=4P, soit P=c²/4 où c désigne le côté du carré. L'aire du petit disque est alors D=pi(r)²=pi(c²/2), et finalement P/D=(c²/4)/[pi(c²/2)]=1/2pi |
 |
des enclos avec 24 clôtures (2000 : I29 et S29)
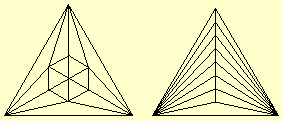
| Comme une clôture ne peut appartenir à plus de deux enclos, pour maximiser le nombre d'enclos il faut minimiser le nombre de clôtures extérieures (qui n'appartiennent qu'à un seul enclos), donc choisir un triangle. De même on peut réaliser davantage d'enclos triangulaires plutôt que d'autres formes polygonales.
Il suffit donc de partager un triangle en triangles en utilisant 24 segments. Voici deux configurations possibles de 15 enclos. |
 |
des polyèdres à faces triangulaires et carrées (2000 : J30, I30 et S30)
|
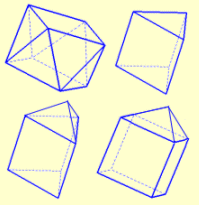
Quand on assemble deux polygones, deux côtés forment une arête ; le nombre total de côtés doit donc être pair, d'où l'impossibilité de réaliser le quatrième assemblage.
Les quatre autres permettent d'assembler, dans l'ordre de l'énoncé, un antiprisme carré, un prisme triangulaire, un tel prisme et un tétraèdre avec une face triangulaire commune ("maison triangulaire avec toit à trois pans"), un cube et une pyramide avec une face carrée commune ("maison carrée avec toit à quatre pans").
Cette question a embarrassé beaucoup d'excellents élèves qui avaient répondu correctement aux 29 questions précédentes ; la recherche de la solution ne nécessite pourtant que quelques connaissances élémentaires (quiconque s'est un peu intéressé aux polyèdres connaît les antiprismes). |
 |